

In mathematics we say if
This means the statement
Now let's say set S is equal to all positive even numbers:
S = {2,4,6,8...}
If the above statement is true, then the following statements are also true:
1) 3 ∉ S
2) 100 ∈ S
3) 97 ∉S
4) 8 ∈ S
There are two ways you can define a set.
Sets are said to be equal if they both contain the exact same elements.
Y = {6,66,666}
Set X is equal to set Y:
If sets X and Y are equal and 6 is an element of X, then 6 must also be an element of Y. Similarly, if 42 is not an element in X, then it is not an element in Y.
If all of A's elements are also contained in B, then A is a subset of B:
If A is a subset of B and B is a subset of A, then A and B are equal sets:
If a set holds no values it is said to be empty or null:
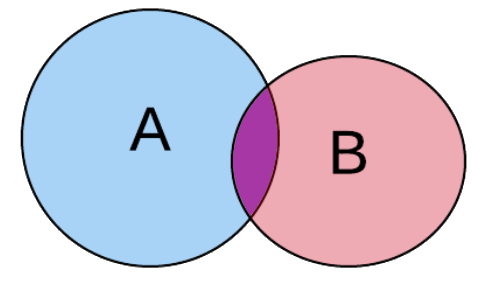
A union B means all of the elements that are contained in A or B. If an element exists in A, it is included in this union. If x exists in B, it is also included in this union.
If x exists in both A and B, it exists in this union.
Picture a man and woman getting married. The man comes from family A and the woman comes from family B. The union of family A and B is all the members of both families.
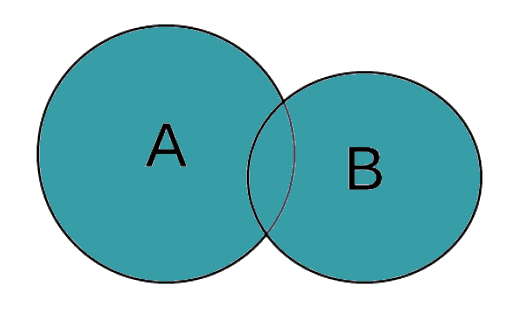
The intersection between A and B is equal to all elements found in A that also found in B. If group A is all Americans who speak Japanese and group B is all Americans who speak Spanish, the intercetion of groups A and B is all Americans who speak Spanish and Japanese.
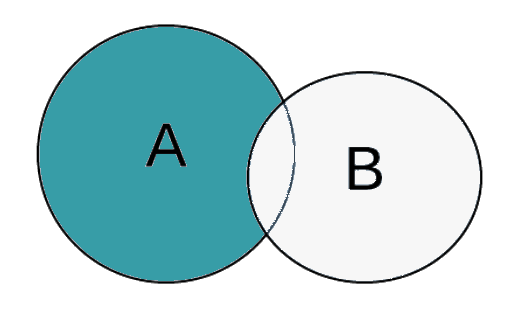
A minus B equals all the elements in A that are NOT contained in B. Let's say Group A is American voters and Group B is Americans who voted for Donald Trump. Group A minus Group B is all the American voters who did Not vote for Donald Trump.
If you want to learn more about logic, check out Logic for Programmers. This page includes aditional logic videos and a logic quiz game!